Bir üçgenin alanı nasıl bulunur? Bir üçgenin alanı nasıl hesaplanır? Üç tarafa ve çevrel dairenin yarıçapına dayalı bir üçgenin alanı için formül

06.03.2022 | Kırık ve morarma

Taban ve yükseklik bilinerek bulunabilir. Diyagramın tüm basitliği, yüksekliğin a tabanını a 1 ve a 2 olmak üzere iki parçaya ve üçgenin kendisini alanı ve olan iki dik üçgene bölmesinde yatmaktadır. Daha sonra tüm üçgenin alanı belirtilen iki alanın toplamı olacaktır ve eğer yüksekliğin bir saniyesini braketten çıkarırsak, toplamda tabanı geri alırız:

Hesaplamalar için daha zor bir yöntem, üç tarafı da bilmeniz gereken Heron formülüdür. Bu formül için öncelikle üçgenin yarı çevresini hesaplamanız gerekir: Heron formülünün kendisi, yarı çevrenin karekökünün her iki taraftaki farkla çarpılmasını ifade eder.

Herhangi bir üçgen için de geçerli olan aşağıdaki yöntem, üçgenin alanını iki kenardan ve aralarındaki açıyı bulmanızı sağlar. Bunun kanıtı yükseklik formülünden gelir - bilinen kenarlardan herhangi birinin yüksekliğini çizeriz ve α açısının sinüsü aracılığıyla h=a⋅sinα sonucunu elde ederiz. Alanı hesaplamak için yüksekliğin yarısını ikinci kenarla çarpın.

Diğer bir yol ise 2 açıyı ve aralarındaki kenarı bilerek üçgenin alanını bulmaktır. Bu formülün ispatı oldukça basittir ve diyagramdan açıkça görülebilmektedir.

Üçüncü açının tepe noktasından yüksekliği bilinen tarafa indiririz ve ortaya çıkan parçalara buna göre x adını veririz. Dik üçgenlerden birinci segment x'in çarpıma eşit olduğu görülebilir.

Üçgen, aynı düz çizgi üzerinde yer almayan noktaları birleştiren üç düz çizgiden oluşan geometrik bir şekildir. Çizgilerin bağlantı noktaları, Latin harfleriyle (örneğin A, B, C) gösterilen üçgenin köşeleridir. Bir üçgenin birbirine bağlanan düz çizgilerine bölümler denir ve bunlar genellikle Latin harfleriyle de gösterilir. Aşağıdaki üçgen türleri ayırt edilir:

Dikdörtgen.
Geniş.
Akut açısal.
Çok yönlü.
Eşkenar.
İkizkenar.

Bir üçgenin alanını hesaplamak için genel formüller

Uzunluk ve yüksekliğe dayalı bir üçgenin alanı için formül

S= a*h/2,
burada a, alanı bulunması gereken üçgenin kenar uzunluğu, h ise tabana çizilen yüksekliğin uzunluğudur.

Heron'un formülü

S=√р*(р-а)*(р-b)*(p-c),
burada √ karekök, p üçgenin yarı çevresi, a,b,c üçgenin her bir tarafının uzunluğudur. Bir üçgenin yarı çevresi p=(a+b+c)/2 formülü kullanılarak hesaplanabilir.

Segmentin açısına ve uzunluğuna dayalı bir üçgenin alanı için formül

S = (a*b*sin(α))/2,
burada b,c üçgenin kenarlarının uzunluğudur, sin(α) iki kenar arasındaki açının sinüsüdür.

Yazılı dairenin yarıçapı ve üç tarafı verilen bir üçgenin alanı için formül

S=p*r,
burada p, alanı bulunması gereken üçgenin yarı çevresidir, r ise bu üçgenin içine yazılan dairenin yarıçapıdır.

Üç kenara dayalı bir üçgenin alanı ve etrafını çevreleyen dairenin yarıçapı için formül

S= (a*b*c)/4*R,
burada a,b,c üçgenin her bir tarafının uzunluğudur, R ise üçgenin etrafını çevreleyen dairenin yarıçapıdır.

Noktaların Kartezyen koordinatlarını kullanan üçgenin alanı formülü

Noktaların kartezyen koordinatları xOy sistemindeki koordinatlardır; burada x apsis, y ise ordinattır. Bir düzlemdeki Kartezyen koordinat sistemi xOy, ortak orijini O noktasında olan, karşılıklı dik Ox ve Oy sayısal eksenleridir. Bu düzlemdeki noktaların koordinatları A(x1, y1), B(x2, y2) şeklinde verilirse ) ve C(x3, y3 ) ise, iki vektörün vektör çarpımından elde edilen aşağıdaki formülü kullanarak üçgenin alanını hesaplayabilirsiniz.
S = |(x1 – x3) (y2 – y3) – (x2 – x3) (y1 – y3)|/2,
nerede || modül anlamına gelir.

Dik üçgenin alanı nasıl bulunur

Dik üçgen, bir açısı 90 derece olan üçgendir. Bir üçgenin yalnızca bir tane böyle açısı olabilir.

İki taraftaki dik üçgenin alanı için formül

S= a*b/2,
burada a,b bacakların uzunluğudur. Bacaklar dik açıya bitişik kenarlardır.

Hipotenüs ve dar açıya dayalı dik üçgenin alanı formülü

S = a*b*sin(α)/ 2,
burada a, b üçgenin bacaklarıdır ve sin(α), a, b doğrularının kesiştiği açının sinüsüdür.

Yan ve karşı açıya göre dik üçgenin alanı formülü

S = a*b/2*tg(β),
burada a, b üçgenin bacaklarıdır, tan(β), a, b bacaklarının birleştiği açının tanjantıdır.

İkizkenar üçgenin alanı nasıl hesaplanır

İkizkenar üçgen, iki eşit kenarı olan bir üçgendir. Bu taraflara kenar, diğer tarafa ise taban denir. İkizkenar üçgenin alanını hesaplamak için aşağıdaki formüllerden birini kullanabilirsiniz.

İkizkenar üçgenin alanını hesaplamak için temel formül

S=h*c/2,
burada c üçgenin tabanıdır, h ise üçgenin tabana indirilen yüksekliğidir.

Kenar ve tabana dayalı ikizkenar üçgen formülü

S=(c/2)* √(a*a – c*c/4),
burada c üçgenin tabanıdır, a ise ikizkenar üçgenin kenarlarından birinin boyutudur.

Eşkenar üçgenin alanı nasıl bulunur

Eşkenar üçgen, tüm kenarların eşit olduğu bir üçgendir. Eşkenar üçgenin alanını hesaplamak için aşağıdaki formülü kullanabilirsiniz:
S = (√3*a*a)/4,
burada a eşkenar üçgenin kenarının uzunluğudur.

Yukarıdaki formüller üçgenin gerekli alanını hesaplamanıza izin verecektir. Üçgenin alanını hesaplamak için üçgenin türünü ve hesaplama için kullanılabilecek mevcut verileri dikkate almanız gerektiğini unutmamak önemlidir.

Alan kavramı

Herhangi bir geometrik şeklin, özellikle bir üçgenin alanı kavramı, kare gibi bir şekil ile ilişkilendirilecektir. Herhangi bir geometrik şeklin birim alanı için, kenarı bire eşit olan karenin alanını alacağız. Bütünlüğü sağlamak için geometrik şekillerin alanları kavramının iki temel özelliğini hatırlayalım.

Özellik 1: Geometrik şekillerin eşit olması durumunda alanları da eşittir.

Özellik 2: Herhangi bir rakam birkaç rakama bölünebilir. Ayrıca orijinal şeklin alanı, onu oluşturan tüm şekillerin alanlarının toplamına eşittir.

Bir örneğe bakalım.

örnek 1

Açıkçası, üçgenin kenarlarından biri bir dikdörtgenin köşegenidir, bir kenarının uzunluğu 5$'dır (çünkü $5$ hücreleri vardır), diğeri $6$'dır (çünkü $6$ hücreleri vardır). Dolayısıyla bu üçgenin alanı böyle bir dikdörtgenin yarısına eşit olacaktır. Dikdörtgenin alanı

O zaman üçgenin alanı eşittir

Cevap: 15$.

Daha sonra, üçgenlerin alanlarını bulmak için çeşitli yöntemleri ele alacağız; yani yüksekliği ve tabanı kullanarak, Heron formülünü ve eşkenar üçgenin alanını kullanarak.

Yüksekliğini ve tabanını kullanarak bir üçgenin alanı nasıl bulunur?

Teorem 1

Bir üçgenin alanı, bir kenar uzunluğu ile o kenar yüksekliğinin çarpımının yarısı kadar bulunabilir.

Matematiksel olarak şöyle görünüyor

$S=\frac(1)(2)αh$

burada $a$ kenarın uzunluğu, $h$ ona çizilen yüksekliktir.

Kanıt.

$AC=α$ olan bir $ABC$ üçgenini düşünün. Bu tarafa $h$'a eşit olan $BH$ yüksekliği çizilir. Şekil 2'deki gibi $AXYC$ karesine kadar oluşturalım.

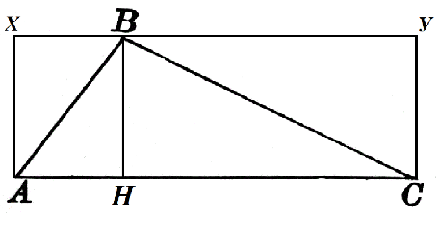
$AXBH$ dikdörtgeninin alanı $h\cdot AH$ ve $HBYC$ dikdörtgeninin alanı $h\cdot HC$'dir. Daha sonra

$S_ABH=\frac(1)(2)h\cdot AH$, $S_CBH=\frac(1)(2)h\cdot HC$

Bu nedenle, özellik 2'ye göre üçgenin gerekli alanı şuna eşittir:

$S=S_ABH+S_CBH=\frac(1)(2)h\cdot AH+\frac(1)(2)h\cdot HC=\frac(1)(2)h\cdot (AH+HC)=\ frac(1)(2)αh$

Teorem kanıtlandı.

Örnek 2

Hücrenin alanı bire eşitse aşağıdaki şekildeki üçgenin alanını bulun

Bu üçgenin tabanı $9$'a eşittir (çünkü $9$, $9$'ın karesidir). Yükseklik de 9$'dır. O zaman Teorem 1'e göre şunu elde ederiz:

$S=\frac(1)(2)\cdot 9\cdot 9=40,5$

Cevap: 40,5$.

Heron'un formülü

Teorem 2

Bize $α$, $β$ ve $γ$ üçgeninin üç kenarı verilirse, alanı aşağıdaki gibi bulunabilir.

$S=\sqrt(ρ(ρ-α)(ρ-β)(ρ-γ))$

burada $ρ$ bu üçgenin yarı çevresi anlamına geliyor.

Kanıt.

Aşağıdaki şekli göz önünde bulundurun:

Pisagor teoremine göre $ABH$ üçgeninden şunu elde ederiz:

Pisagor teoremine göre $CBH$ üçgeninden şunu elde ederiz:

$h^2=α^2-(β-x)^2$

$h^2=α^2-β^2+2βx-x^2$

Bu iki ilişkiden eşitliği elde ederiz

$γ^2-x^2=α^2-β^2+2βx-x^2$

$x=\frac(γ^2-α^2+β^2)(2β)$

$h^2=γ^2-(\frac(γ^2-α^2+β^2)(2β))^2$

$h^2=\frac((α^2-(γ-β)^2)((γ+β)^2-α^2))(4β^2)$

$h^2=\frac((α-γ+β)(α+γ-β)(γ+β-α)(γ+β+α))(4β^2)$

$ρ=\frac(α+β+γ)(2)$ olduğundan $α+β+γ=2ρ$, yani

$h^2=\frac(2ρ(2ρ-2γ)(2ρ-2β)(2ρ-2α))(4β^2)$

$h^2=\frac(4ρ(ρ-α)(ρ-β)(ρ-γ))(β^2 )$

$h=\sqrt(\frac(4ρ(ρ-α)(ρ-β)(ρ-γ))(β^2))$

$h=\frac(2)(β)\sqrt(ρ(ρ-α)(ρ-β)(ρ-γ))$

Teorem 1'e göre şunu elde ederiz:

$S=\frac(1)(2) βh=\frac(β)(2)\cdot \frac(2)(β) \sqrt(ρ(ρ-α)(ρ-β)(ρ-γ) )=\sqrt(ρ(ρ-α)(ρ-β)(ρ-γ))$

Bazen hayatta, uzun süredir unutulmuş okul bilgisini aramak için hafızanızı araştırmanız gereken durumlar vardır. Örneğin, üçgen şeklindeki bir arsanın alanını belirlemeniz gerekiyor veya bir apartman dairesinde veya özel evde başka bir yenileme zamanı geldi ve yüzey için ne kadar malzemeye ihtiyaç duyulacağını hesaplamanız gerekiyor. üçgen bir şekil. Böyle bir problemi birkaç dakika içinde çözebileceğiniz bir zaman vardı, ama şimdi umutsuzca bir üçgenin alanını nasıl belirleyeceğinizi hatırlamaya mı çalışıyorsunuz?

Endişelenmeyin! Sonuçta, bir kişinin beyninin uzun süredir kullanılmayan bilgiyi bir yere uzak bir köşeye aktarmaya karar vermesi oldukça normaldir ve bazen onu çıkarmak o kadar kolay değildir. Böyle bir sorunu çözmek için unutulmuş okul bilgilerini aramakla uğraşmanıza gerek kalmaması için bu makale, üçgenin gerekli alanını bulmayı kolaylaştıran çeşitli yöntemler içermektedir.

Bir üçgenin mümkün olan en az kenar sayısıyla sınırlı bir çokgen türü olduğu iyi bilinmektedir. Prensip olarak, herhangi bir çokgen, köşelerini kenarlarıyla kesişmeyen bölümlere bağlayarak birkaç üçgene bölünebilir. Bu nedenle üçgeni bilerek neredeyse her şeklin alanını hesaplayabilirsiniz.

Hayatta meydana gelebilecek tüm olası üçgenler arasında aşağıdaki özel türler ayırt edilebilir: ve dikdörtgen.

Bir üçgenin alanını hesaplamanın en kolay yolu, açılarından birinin dik olması, yani dik üçgen olması durumundadır. Yarım dikdörtgen olduğunu görmek kolaydır. Dolayısıyla alanı birbirine dik açı oluşturan kenarların çarpımının yarısına eşittir.

Bir üçgenin bir köşesinden karşı kenara indirilen yüksekliğini ve taban denilen bu kenarın uzunluğunu bilirsek alan, yükseklik ile tabanın çarpımının yarısı kadar hesaplanır. Bu, aşağıdaki formül kullanılarak yazılmıştır:

S = 1/2*b*h, burada

S üçgenin gerekli alanıdır;

b, h - sırasıyla üçgenin yüksekliği ve tabanı.

Bir ikizkenar üçgenin alanını hesaplamak çok kolaydır çünkü yükseklik karşı kenarı ikiye böler ve kolaylıkla ölçülebilir. Alanın belirlenmesi durumunda dik açı oluşturan kenarlardan birinin uzunluğunun yükseklik olarak alınması uygun olur.

Bütün bunlar elbette güzel ama bir üçgenin açılarından birinin doğru olup olmadığı nasıl belirlenecek? Figürümüzün boyutu küçükse inşaat açısı, çizim üçgeni, kartpostal veya dikdörtgen şekilli başka bir nesne kullanabiliriz.

Peki ya üçgen bir arsamız varsa? Bu durumda şu şekilde ilerleyin: bir tarafta varsayılan dik açının tepesinden itibaren 3'ün katları olan mesafeyi (30 cm, 90 cm, 3 m) sayın ve diğer tarafta aynı şekilde 4'ün katları olan mesafeyi ölçün. orantı (40 cm, 160 cm, 4 m). Şimdi bu iki parçanın uç noktaları arasındaki mesafeyi ölçmeniz gerekiyor. Sonuç 5'in katı ise (50 cm, 250 cm, 5 m) açının doğru olduğunu söyleyebiliriz.

Şeklimizin üç tarafının her birinin uzunluğu biliniyorsa, üçgenin alanı Heron formülü kullanılarak belirlenebilir. Daha basit bir forma sahip olması için yarı çevre adı verilen yeni bir değer kullanılır. Bu, üçgenimizin tüm kenarlarının toplamının ikiye bölünmesidir. Yarı çevre hesaplandıktan sonra aşağıdaki formülü kullanarak alanı belirlemeye başlayabilirsiniz:

S = sqrt(p(p-a)(p-b)(p-c))), burada

sqrt - karekök;

p - yarı çevre değeri (p = (a+b+c)/2);

a, b, c - üçgenin kenarları (yanları).

Peki ya üçgenin şekli düzensizse? Burada iki olası yol var. Bunlardan ilki, böyle bir şekli, alanlarının toplamı ayrı ayrı hesaplanıp daha sonra eklenen iki dik üçgene bölmeye çalışmaktır. Veya iki kenar arasındaki açı ve bu kenarların boyutu biliniyorsa aşağıdaki formülü uygulayın:

S = 0,5 * ab * sinC, burada

a,b - üçgenin kenarları;

c bu kenarlar arasındaki açının boyutudur.

İkinci durum pratikte nadirdir, ancak yine de hayatta her şey mümkündür, bu nedenle yukarıdaki formül gereksiz olmayacaktır. Hesaplamalarınızda iyi şanslar!

Bir üçgenin alanı. Alan hesaplamasını içeren birçok geometri probleminde üçgenin alanı için formüller kullanılır. Bunlardan birkaçı var, burada ana olanlara bakacağız.Bu formülleri listelemek çok basit olur ve hiçbir işe yaramaz. En sık kullanılan temel formüllerin kökenini analiz edeceğiz.

Formüllerin türetilmesini okumadan önce ilgili makaleye mutlaka bakın.Materyali inceledikten sonra, formülleri hafızanıza kolayca geri yükleyebilirsiniz (ihtiyaç duyduğunuz anda aniden "uçup giderlerse").

İlk formül

Paralelkenarın köşegeni onu eşit alanlı iki üçgene böler:

Bu nedenle üçgenin alanı paralelkenarın alanının yarısına eşit olacaktır:

Üçgenin alanı formülü

*Yani üçgenin herhangi bir kenarını ve bu kenara indirilen yüksekliği biliyorsak, bu üçgenin alanını her zaman hesaplayabiliriz.

Formül iki

Paralelkenarın alanıyla ilgili makalede daha önce belirtildiği gibi formül şöyle görünür:

Bir üçgenin alanı, alanının yarısına eşittir, bu şu anlama gelir:

*Yani bir üçgenin herhangi iki kenarı ve aralarındaki açı biliniyorsa, böyle bir üçgenin alanını her zaman hesaplayabiliriz.

Heron formülü (üçüncü)

Bu formülün elde edilmesi zordur ve işinize yaramaz. Bakın ne kadar güzel, kendisinin unutulmaz olduğunu söyleyebilirsiniz.

*Bir üçgenin üç kenarı verilmişse bu formülü kullanarak üçgenin alanını her zaman hesaplayabiliriz.

Formül dört

Nerede R– yazılı dairenin yarıçapı

*Bir üçgenin üç kenarı ve içine yazılan dairenin yarıçapı biliniyorsa bu üçgenin alanını her zaman bulabiliriz.

Formül beş

Nerede R– çevrelenmiş dairenin yarıçapı.

*Bir üçgenin üç kenarı ve onu çevreleyen dairenin yarıçapı biliniyorsa, böyle bir üçgenin alanını her zaman bulabiliriz.

Şu soru ortaya çıkıyor: Bir üçgenin üç tarafı biliniyorsa, Heron formülünü kullanarak alanını bulmak daha kolay değil mi?

Evet, daha kolay olabilir ama her zaman değil, bazen karmaşıklık ortaya çıkabilir. Bu, kökün çıkarılmasını içerir. Ayrıca bu formüller, bir üçgenin alanının ve kenarlarının verildiği ve yazılı veya çevrelenmiş dairenin yarıçapını bulmanız gereken problemlerde kullanıma çok uygundur. Bu tür görevler Birleşik Devlet Sınavının bir parçası olarak mevcuttur.

Formüle ayrı ayrı bakalım:

İçine bir dairenin yazıldığı bir çokgenin alanı için formülün özel bir halidir:

Beşgen örneğini kullanarak bunu düşünelim:

Çemberin merkezini bu beşgenin köşelerine bağlayalım ve merkezden yanlara doğru indiren dikmeler yapalım. Düşürülmüş dikmeler yazılı dairenin yarıçapları olacak şekilde beş üçgen elde ediyoruz: