Como encontrar a área de um triângulo. Como calcular a área de um triângulo? Fórmula para a área de um triângulo com base em três lados e no raio do círculo circunscrito

Pode ser encontrado conhecendo a base e a altura. Toda a simplicidade do diagrama reside no fato de que a altura divide a base a em duas partes a 1 e a 2, e o próprio triângulo em dois triângulos retângulos, cuja área é e. Então a área de todo o triângulo será a soma das duas áreas indicadas, e se tirarmos um segundo da altura do colchete, na soma obtemos de volta a base:

Um método de cálculo mais difícil é a fórmula de Heron, para a qual você precisa conhecer todos os três lados. Para esta fórmula, primeiro você precisa calcular o semiperímetro do triângulo: A própria fórmula de Heron implica a raiz quadrada do semiperímetro, multiplicada por sua vez por sua diferença em cada lado.

O método a seguir, também relevante para qualquer triângulo, permite encontrar a área do triângulo através de dois lados e o ângulo entre eles. A prova disso vem da fórmula com altura - traçamos a altura em qualquer um dos lados conhecidos e através do seno do ângulo α obtemos que h=a⋅sinα. Para calcular a área, multiplique metade da altura pelo segundo lado.

Outra forma é encontrar a área de um triângulo, conhecendo 2 ângulos e o lado entre eles. A prova desta fórmula é bastante simples e pode ser vista claramente no diagrama.

Baixamos a altura do vértice do terceiro ângulo para o lado conhecido e chamamos os segmentos resultantes de x de acordo. Dos triângulos retângulos pode-se ver que o primeiro segmento x é igual ao produto

Um triângulo é uma figura geométrica que consiste em três linhas retas conectadas em pontos que não estão na mesma linha reta. Os pontos de conexão das linhas são os vértices do triângulo, que são designados por letras latinas (por exemplo, A, B, C). As linhas retas que conectam um triângulo são chamadas de segmentos, que também são geralmente denotados por letras latinas. Os seguintes tipos de triângulos são diferenciados:

• Retangular.
• Obtuso.
• Angular agudo.
• Versátil.
• Equilátero.
• Isósceles.

Fórmulas gerais para calcular a área de um triângulo

Fórmula para a área de um triângulo com base no comprimento e altura

S= a*h/2,
onde a é o comprimento do lado do triângulo cuja área precisa ser encontrada, h é o comprimento da altura desenhada até a base.

Fórmula de Heron

S=√р*(р-а)*(р-b)*(p-c),
onde √ é a raiz quadrada, p é o semiperímetro do triângulo, a,b,c é o comprimento de cada lado do triângulo. O semiperímetro de um triângulo pode ser calculado usando a fórmula p=(a+b+c)/2.

Fórmula para a área de um triângulo com base no ângulo e no comprimento do segmento

S = (a*b*sin(α))/2,
onde b,c é o comprimento dos lados do triângulo, sin(α) é o seno do ângulo entre os dois lados.

Fórmula para a área de um triângulo dado o raio do círculo inscrito e três lados

S=p*r,
onde p é o semiperímetro do triângulo cuja área precisa ser encontrada, r é o raio do círculo inscrito neste triângulo.

Fórmula para a área de um triângulo com base em três lados e no raio do círculo circunscrito ao seu redor

S= (a*b*c)/4*R,
onde a,b,c é o comprimento de cada lado do triângulo, R é o raio do círculo circunscrito ao redor do triângulo.

Fórmula para a área de um triângulo usando as coordenadas cartesianas dos pontos

As coordenadas cartesianas dos pontos são coordenadas no sistema xOy, onde x é a abcissa, y é a ordenada. O sistema de coordenadas cartesianas xOy em um plano são os eixos numéricos mutuamente perpendiculares Ox e Oy com uma origem comum no ponto O. Se as coordenadas dos pontos neste plano são dadas na forma A(x1, y1), B(x2, y2 ) e C(x3, y3 ), então você pode calcular a área do triângulo usando a seguinte fórmula, que é obtida a partir do produto vetorial de dois vetores.
S = |(x1 – x3) (y2 – y3) – (x2 – x3) (y1 – y3)|/2,
onde || significa módulo.

Como encontrar a área de um triângulo retângulo

Um triângulo retângulo é um triângulo com um ângulo medindo 90 graus. Um triângulo só pode ter um desses ângulos.

Fórmula para a área de um triângulo retângulo em dois lados

S = a*b/2,
onde a,b é o comprimento das pernas. Pernas são os lados adjacentes a um ângulo reto.

Fórmula para a área de um triângulo retângulo baseada na hipotenusa e no ângulo agudo

S = a*b*sin(α)/ 2,
onde a, b são os catetos do triângulo e sin(α) é o seno do ângulo no qual as retas a, b se cruzam.

Fórmula para a área de um triângulo retângulo com base no lado e no ângulo oposto

S = a*b/2*tg(β),
onde a, b são os catetos do triângulo, tan(β) é a tangente do ângulo no qual os catetos a, b estão conectados.

Como calcular a área de um triângulo isósceles

Um triângulo isósceles é aquele que possui dois lados iguais. Esses lados são chamados de lados e o outro lado é a base. Para calcular a área de um triângulo isósceles, você pode usar uma das seguintes fórmulas.

Fórmula básica para calcular a área de um triângulo isósceles

S=h*c/2,
onde c é a base do triângulo, h é a altura do triângulo abaixado até a base.

Fórmula de um triângulo isósceles com base no lado e na base

S=(c/2)* √(a*a – c*c/4),
onde c é a base do triângulo, a é o tamanho de um dos lados laterais do triângulo isósceles.

Como encontrar a área de um triângulo equilátero

Um triângulo equilátero é um triângulo em que todos os lados são iguais. Para calcular a área de um triângulo equilátero, você pode usar a seguinte fórmula:
S = (√3*a*a)/4,
onde a é o comprimento do lado do triângulo equilátero.

As fórmulas acima permitirão calcular a área necessária do triângulo. É importante lembrar que para calcular a área dos triângulos é preciso considerar o tipo de triângulo e os dados disponíveis que podem ser utilizados para o cálculo.

Conceito de área

O conceito de área de qualquer figura geométrica, em particular de um triângulo, estará associado a uma figura como um quadrado. Para a área unitária de qualquer figura geométrica tomaremos a área de um quadrado cujo lado é igual a um. Para completar, vamos relembrar duas propriedades básicas para o conceito de áreas de figuras geométricas.

Propriedade 1: Se as figuras geométricas forem iguais, então suas áreas também serão iguais.

Propriedade 2: Qualquer figura pode ser dividida em várias figuras. Além disso, a área da figura original é igual à soma das áreas de todas as suas figuras constituintes.

Vejamos um exemplo.

Exemplo 1

Obviamente, um dos lados do triângulo é uma diagonal de um retângulo, um lado do qual tem comprimento de $5$ (já que há $5$ células) e o outro tem $6$ (já que há $6$ células). Portanto, a área deste triângulo será igual à metade desse retângulo. A área do retângulo é

Então a área do triângulo é igual a

Resposta: $ 15 $.

A seguir, consideraremos vários métodos para encontrar as áreas dos triângulos, nomeadamente utilizando a altura e a base, utilizando a fórmula de Heron e a área de um triângulo equilátero.

Como encontrar a área de um triângulo usando sua altura e base

Teorema 1

A área de um triângulo pode ser encontrada como metade do produto do comprimento de um lado pela altura desse lado.

Matematicamente é assim

$S=\frac(1)(2)αh$

onde $a$ é o comprimento do lado, $h$ é a altura desenhada para ele.

Prova.

Considere um triângulo $ABC$ em que $AC=α$. A altura $BH$ é desenhada para este lado, que é igual a $h$. Vamos construí-lo até o quadrado $AXYC$ como na Figura 2.

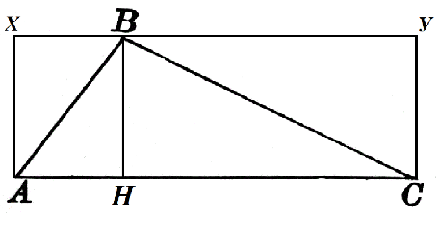
A área do retângulo $AXBH$ é $h\cdot AH$, e a área do retângulo $HBYC$ é $h\cdot HC$. Então

$S_ABH=\frac(1)(2)h\cdot AH$, $S_CBH=\frac(1)(2)h\cdot HC$

Portanto, a área necessária do triângulo, pela propriedade 2, é igual a

$S=S_ABH+S_CBH=\frac(1)(2)h\cdot AH+\frac(1)(2)h\cdot HC=\frac(1)(2)h\cdot (AH+HC)=\ frac(1)(2)αh$

O teorema está provado.

Exemplo 2

Encontre a área do triângulo na figura abaixo se a célula tiver uma área igual a um

A base deste triângulo é igual a $9$ (já que $9$ são $9$ quadrados). A altura também é $ 9$. Então, pelo Teorema 1, obtemos

$S=\frac(1)(2)\cponto 9\cponto 9=40,5$

Resposta: $ 40,5 $.

Fórmula de Heron

Teorema 2

Se tivermos três lados de um triângulo $α$, $β$ e $γ$, então sua área pode ser encontrada da seguinte forma

$S=\sqrt(ρ(ρ-α)(ρ-β)(ρ-γ))$

aqui $ρ$ significa o semiperímetro deste triângulo.

Prova.

Considere a seguinte figura:

Pelo teorema de Pitágoras, do triângulo $ABH$ obtemos

Do triângulo $CBH$, segundo o teorema de Pitágoras, temos

$h^2=α^2-(β-x)^2$

$h^2=α^2-β^2+2βx-x^2$

Destas duas relações obtemos a igualdade

$γ^2-x^2=α^2-β^2+2βx-x^2$

$x=\frac(γ^2-α^2+β^2)(2β)$

$h^2=γ^2-(\frac(γ^2-α^2+β^2)(2β))^2$

$h^2=\frac((α^2-(γ-β)^2)((γ+β)^2-α^2))(4β^2)$

$h^2=\frac((α-γ+β)(α+γ-β)(γ+β-α)(γ+β+α))(4β^2)$

Como $ρ=\frac(α+β+γ)(2)$, então $α+β+γ=2ρ$, o que significa

$h^2=\frac(2ρ(2ρ-2γ)(2ρ-2β)(2ρ-2α))(4β^2)$

$h^2=\frac(4ρ(ρ-α)(ρ-β)(ρ-γ))(β^2 )$

$h=\sqrt(\frac(4ρ(ρ-α)(ρ-β)(ρ-γ))(β^2))$

$h=\frac(2)(β)\sqrt(ρ(ρ-α)(ρ-β)(ρ-γ))$

Pelo Teorema 1, obtemos

$S=\frac(1)(2) βh=\frac(β)(2)\cdot \frac(2)(β) \sqrt(ρ(ρ-α)(ρ-β)(ρ-γ) )=\sqrt(ρ(ρ-α)(ρ-β)(ρ-γ))$

Às vezes, na vida, há situações em que é preciso mergulhar na memória em busca de conhecimentos escolares há muito esquecidos. Por exemplo, você precisa determinar a área de um terreno de formato triangular, ou chegou a hora de outra reforma em um apartamento ou casa particular, e precisa calcular quanto material será necessário para uma superfície com uma forma triangular. Houve um tempo em que você poderia resolver esse problema em alguns minutos, mas agora você está tentando desesperadamente se lembrar de como determinar a área de um triângulo?

Não se preocupe com isso! Afinal, é normal quando o cérebro de uma pessoa decide transferir conhecimento há muito não utilizado para algum lugar, para um canto remoto, de onde às vezes não é tão fácil extraí-lo. Para que você não precise se esforçar para encontrar conhecimentos escolares esquecidos para resolver esse problema, este artigo contém vários métodos que facilitam a localização da área necessária de um triângulo.

É bem sabido que um triângulo é um tipo de polígono limitado ao mínimo número possível de lados. Em princípio, qualquer polígono pode ser dividido em vários triângulos conectando seus vértices com segmentos que não cruzam seus lados. Portanto, conhecendo o triângulo, você pode calcular a área de quase qualquer figura.

Entre todos os triângulos possíveis que ocorrem na vida, podem ser distinguidos os seguintes tipos particulares: e retangular.

A maneira mais fácil de calcular a área de um triângulo é quando um de seus ângulos é reto, ou seja, no caso de um triângulo retângulo. É fácil ver que é meio retângulo. Portanto, sua área é igual à metade do produto dos lados que formam um ângulo reto entre si.

Se conhecermos a altura de um triângulo que desce de um de seus vértices até o lado oposto, e o comprimento desse lado, que é chamado de base, então a área é calculada como metade do produto da altura pela base. Isso é escrito usando a seguinte fórmula:

S = 1/2*b*h, em que

S é a área necessária do triângulo;

b, h - respectivamente, a altura e a base do triângulo.

É tão fácil calcular a área de um triângulo isósceles porque a altura dividirá o lado oposto ao meio e pode ser facilmente medida. Se a área for determinada, é conveniente considerar como altura o comprimento de um dos lados formando um ângulo reto.

Tudo isso é bom, claro, mas como determinar se um dos ângulos de um triângulo é reto ou não? Se o tamanho da nossa figura for pequeno, podemos usar um ângulo de construção, um triângulo de desenho, um cartão postal ou outro objeto de formato retangular.

Mas e se tivermos um terreno triangular? Neste caso, proceda da seguinte forma: conte a partir do topo do suposto ângulo reto de um lado uma distância múltipla de 3 (30 cm, 90 cm, 3 m), e do outro lado meça uma distância múltipla de 4 no mesmo proporção (40 cm, 160 cm, 4 m). Agora você precisa medir a distância entre os pontos finais desses dois segmentos. Se o resultado for um múltiplo de 5 (50 cm, 250 cm, 5 m), então podemos dizer que o ângulo está correto.

Se o comprimento de cada um dos três lados da nossa figura for conhecido, então a área do triângulo pode ser determinada usando a fórmula de Heron. Para que tenha uma forma mais simples, é utilizado um novo valor, que é denominado semiperímetro. Esta é a soma de todos os lados do nosso triângulo, dividida ao meio. Após o cálculo do semiperímetro, você pode começar a determinar a área usando a fórmula:

S = sqrt (p (p-a) (p-b) (p-c)), onde

sqrt - raiz quadrada;

p - valor do semiperímetro (p = (a+b+c)/2);

a, b, c - arestas (lados) do triângulo.

Mas e se o triângulo tiver uma forma irregular? Existem duas maneiras possíveis aqui. A primeira delas é tentar dividir tal figura em dois triângulos retângulos, cuja soma das áreas é calculada separadamente e depois somada. Ou, se o ângulo entre dois lados e o tamanho desses lados forem conhecidos, aplique a fórmula:

S = 0,5 * ab * sinC, onde

a,b - lados do triângulo;

c é o tamanho do ângulo entre esses lados.

Este último caso é raro na prática, mas mesmo assim tudo é possível na vida, portanto a fórmula acima não será supérflua. Boa sorte com seus cálculos!

Área de um triângulo. Em muitos problemas de geometria que envolvem o cálculo de áreas, são utilizadas fórmulas para a área de um triângulo. Existem vários deles, aqui veremos os principais.Listar essas fórmulas seria muito simples e inútil. Analisaremos a origem das fórmulas básicas, aquelas que são mais utilizadas.

Antes de ler a derivação das fórmulas, não deixe de ler o artigo sobre.Depois de estudar o material, você pode facilmente restaurar as fórmulas em sua memória (se elas “voarem” de repente no momento que você precisar).

Primeira fórmula

A diagonal de um paralelogramo o divide em dois triângulos de áreas iguais:

Portanto, a área do triângulo será igual à metade da área do paralelogramo:

Fórmula da área do triângulo

*Ou seja, se conhecermos qualquer lado do triângulo e a altura abaixada para esse lado, então sempre poderemos calcular a área desse triângulo.

Fórmula dois

Como já foi dito no artigo sobre a área de um paralelogramo, a fórmula se parece com:

A área de um triângulo é igual à metade de sua área, o que significa:

*Ou seja, se quaisquer dois lados de um triângulo e o ângulo entre eles forem conhecidos, sempre poderemos calcular a área desse triângulo.

Fórmula de Heron (terceira)

Esta fórmula é difícil de derivar e não tem utilidade para você. Olha como ela é linda, podemos dizer que ela mesma é memorável.

*Se forem dados três lados de um triângulo, então usando esta fórmula podemos sempre calcular sua área.

Fórmula quatro

Onde R– raio do círculo inscrito

*Se os três lados de um triângulo e o raio do círculo inscrito nele forem conhecidos, então sempre poderemos encontrar a área desse triângulo.

Fórmula cinco

Onde R– raio do círculo circunscrito.

*Se os três lados de um triângulo e o raio do círculo circunscrito ao seu redor forem conhecidos, então sempre poderemos encontrar a área desse triângulo.

Surge a pergunta: se três lados de um triângulo são conhecidos, não é mais fácil encontrar sua área usando a fórmula de Heron!

Sim, pode ser mais fácil, mas nem sempre, às vezes surge complexidade. Isso envolve extrair a raiz. Além disso, essas fórmulas são muito convenientes para usar em problemas onde a área de um triângulo e seus lados são dados e você precisa encontrar o raio do círculo inscrito ou circunscrito. Essas tarefas estão disponíveis como parte do Exame Estadual Unificado.

Vejamos a fórmula separadamente:

É um caso especial da fórmula da área de um polígono no qual um círculo está inscrito:

Vamos considerar isso usando o exemplo de um pentágono:

Vamos conectar o centro do círculo com os vértices deste pentágono e baixar perpendiculares do centro para seus lados. Obtemos cinco triângulos, com as perpendiculares descartadas sendo os raios do círculo inscrito:

A área do pentágono é:

Agora está claro que se estamos falando de um triângulo, então esta fórmula assume a forma:

Fórmula seis