Comment trouver l'aire d'un triangle. Comment calculer l'aire d'un triangle ? Formule pour l'aire d'un triangle basée sur trois côtés et le rayon du cercle circonscrit

Peut être trouvé en connaissant la base et la hauteur. Toute la simplicité du schéma réside dans le fait que la hauteur divise la base a en deux parties a 1 et a 2, et le triangle lui-même en deux triangles rectangles dont l'aire est et. Ensuite, l'aire du triangle entier sera la somme des deux aires indiquées, et si l'on retire une seconde de la hauteur de la parenthèse, alors dans la somme on récupère la base :

Une méthode de calcul plus difficile est la formule de Heron, pour laquelle vous devez connaître les trois côtés. Pour cette formule, il faut d'abord calculer le demi-périmètre du triangle : La formule de Héron elle-même implique la racine carrée du demi-périmètre, multipliée à son tour par sa différence de chaque côté.

La méthode suivante, également pertinente pour tout triangle, vous permet de trouver l'aire du triangle passant par deux côtés et l'angle entre eux. La preuve en est la formule avec la hauteur - nous dessinons la hauteur sur l'un des côtés connus et par le sinus de l'angle α nous obtenons que h=a⋅sinα. Pour calculer la superficie, multipliez la moitié de la hauteur par le deuxième côté.

Une autre façon consiste à trouver l'aire d'un triangle, en connaissant 2 angles et le côté qui les sépare. La preuve de cette formule est assez simple et peut être clairement visible sur le diagramme.

Nous abaissons la hauteur du sommet du troisième angle jusqu'au côté connu et appelons les segments résultants x en conséquence. A partir des triangles rectangles, on peut voir que le premier segment x est égal au produit

Un triangle est une figure géométrique composée de trois lignes droites reliées par des points qui ne se trouvent pas sur la même ligne droite. Les points de connexion des lignes sont les sommets du triangle, désignés par des lettres latines (par exemple, A, B, C). Les lignes droites reliant un triangle sont appelées segments, qui sont également généralement désignés par des lettres latines. On distingue les types de triangles suivants :

• Rectangulaire.
• Obtus.
• Angulaire aigu.
• Polyvalent.
• Équilatéral.
• Isocèle.

Formules générales pour calculer l'aire d'un triangle

Formule pour l'aire d'un triangle basée sur la longueur et la hauteur

S= une*h/2,
où a est la longueur du côté du triangle dont il faut trouver l'aire, h est la longueur de la hauteur tirée jusqu'à la base.

La formule du héron

S=√р*(р-а)*(р-b)*(pc),
où √ est la racine carrée, p est le demi-périmètre du triangle, a,b,c est la longueur de chaque côté du triangle. Le demi-périmètre d'un triangle peut être calculé à l'aide de la formule p=(a+b+c)/2.

Formule pour l'aire d'un triangle basée sur l'angle et la longueur du segment

S = (a*b*sin(α))/2,
où b,c est la longueur des côtés du triangle, sin(α) est le sinus de l'angle entre les deux côtés.

Formule pour l'aire d'un triangle étant donné le rayon du cercle inscrit et trois côtés

S=p*r,
où p est le demi-périmètre du triangle dont il faut trouver l'aire, r est le rayon du cercle inscrit dans ce triangle.

Formule pour l'aire d'un triangle basée sur trois côtés et le rayon du cercle circonscrit autour de lui

S= (a*b*c)/4*R,
où a,b,c est la longueur de chaque côté du triangle, R est le rayon du cercle circonscrit autour du triangle.

Formule pour l'aire d'un triangle utilisant les coordonnées cartésiennes des points

Les coordonnées cartésiennes des points sont des coordonnées dans le système xOy, où x est l'abscisse, y est l'ordonnée. Le système de coordonnées cartésiennes xOy sur un plan est constitué des axes numériques Ox et Oy mutuellement perpendiculaires ayant une origine commune au point O. Si les coordonnées des points sur ce plan sont données sous la forme A(x1, y1), B(x2, y2 ) et C(x3, y3 ), vous pouvez alors calculer l'aire du triangle à l'aide de la formule suivante, qui est obtenue à partir du produit vectoriel de deux vecteurs.
S = |(x1 – x3) (y2 – y3) – (x2 – x3) (y1 – y3)|/2,
où || signifie module.

Comment trouver l'aire d'un triangle rectangle

Un triangle rectangle est un triangle dont un angle mesure 90 degrés. Un triangle ne peut avoir qu’un seul angle.

Formule pour l'aire d'un triangle rectangle sur deux côtés

S= une*b/2,
où a,b est la longueur des jambes. Les jambes sont les côtés adjacents à un angle droit.

Formule pour l'aire d'un triangle rectangle basée sur l'hypoténuse et l'angle aigu

S = a*b*sin(α)/ 2,
où a, b sont les jambes du triangle et sin(α) est le sinus de l'angle auquel les lignes a, b se coupent.

Formule pour l'aire d'un triangle rectangle basée sur le côté et l'angle opposé

S = une*b/2*tg(β),
où a, b sont les branches du triangle, tan(β) est la tangente de l'angle auquel les branches a, b sont connectées.

Comment calculer l'aire d'un triangle isocèle

Un triangle isocèle est un triangle qui possède deux côtés égaux. Ces côtés sont appelés les côtés et l’autre côté est la base. Pour calculer l'aire d'un triangle isocèle, vous pouvez utiliser l'une des formules suivantes.

Formule de base pour calculer l'aire d'un triangle isocèle

S=h*c/2,
où c est la base du triangle, h est la hauteur du triangle abaissé jusqu'à la base.

Formule d'un triangle isocèle basée sur le côté et la base

S=(c/2)* √(a*a – c*c/4),
où c est la base du triangle, a est la taille de l'un des côtés du triangle isocèle.

Comment trouver l'aire d'un triangle équilatéral

Un triangle équilatéral est un triangle dont tous les côtés sont égaux. Pour calculer l'aire d'un triangle équilatéral, vous pouvez utiliser la formule suivante :
S = (√3*a*a)/4,
où a est la longueur du côté du triangle équilatéral.

Les formules ci-dessus vous permettront de calculer l'aire requise du triangle. Il est important de se rappeler que pour calculer l'aire des triangles, vous devez prendre en compte le type de triangle et les données disponibles qui peuvent être utilisées pour le calcul.

Notion de zone

La notion d'aire de toute figure géométrique, notamment d'un triangle, sera associée à une figure telle qu'un carré. Pour l'aire unitaire de toute figure géométrique, nous prendrons l'aire d'un carré dont le côté est égal à un. Pour être complet, rappelons deux propriétés fondamentales de la notion d'aires de figures géométriques.

Propriété 1 : Si les figures géométriques sont égales, alors leurs aires sont également égales.

Propriété 2 : Toute figure peut être divisée en plusieurs figures. De plus, l'aire de la figure originale est égale à la somme des aires de toutes ses figures constitutives.

Regardons un exemple.

Exemple 1

Évidemment, l'un des côtés du triangle est une diagonale d'un rectangle dont un côté a une longueur de 5$ (puisqu'il y a des cellules de 5$) et l'autre est de 6$ (puisqu'il y a des cellules de 6$). Par conséquent, l'aire de ce triangle sera égale à la moitié d'un tel rectangle. L'aire du rectangle est

Alors l'aire du triangle est égale à

Réponse : 15$.

Ensuite, nous examinerons plusieurs méthodes pour trouver les aires des triangles, à savoir en utilisant la hauteur et la base, en utilisant la formule de Heron et l'aire d'un triangle équilatéral.

Comment trouver l'aire d'un triangle en utilisant sa hauteur et sa base

Théorème 1

L'aire d'un triangle peut être trouvée comme la moitié du produit de la longueur d'un côté et de la hauteur de ce côté.

Mathématiquement, ça ressemble à ça

$S=\frac(1)(2)αh$

où $a$ est la longueur du côté, $h$ est la hauteur qui y est dessinée.

Preuve.

Considérons un triangle $ABC$ dans lequel $AC=α$. La hauteur $BH$ est tracée de ce côté, ce qui est égal à $h$. Construisons-le jusqu'au carré $AXYC$ comme dans la figure 2.

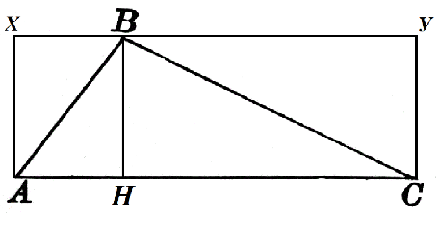
L'aire du rectangle $AXBH$ est $h\cdot AH$, et l'aire du rectangle $HBYC$ est $h\cdot HC$. Alors

$S_ABH=\frac(1)(2)h\cdot AH$, $S_CBH=\frac(1)(2)h\cdot HC$

Par conséquent, l'aire requise du triangle, par la propriété 2, est égale à

$S=S_ABH+S_CBH=\frac(1)(2)h\cdot AH+\frac(1)(2)h\cdot HC=\frac(1)(2)h\cdot (AH+HC)=\ frac(1)(2)αh$

Le théorème a été prouvé.

Exemple 2

Trouvez l'aire du triangle dans la figure ci-dessous si la cellule a une aire égale à un

La base de ce triangle est égale à 9$ (puisque 9$ sont des carrés de 9$). La hauteur est également de 9$. Alors, d'après le théorème 1, on obtient

$S=\frac(1)(2)\cdot 9\cdot 9=40,5$

Réponse : 40,5$.

La formule du héron

Théorème 2

Si on nous donne trois côtés d'un triangle $α$, $β$ et $γ$, alors son aire peut être trouvée comme suit

$S=\sqrt(ρ(ρ-α)(ρ-β)(ρ-γ))$

ici $ρ$ signifie le demi-périmètre de ce triangle.

Preuve.

Considérons la figure suivante :

D'après le théorème de Pythagore, à partir du triangle $ABH$ on obtient

A partir du triangle $CBH$, d'après le théorème de Pythagore, on a

$h^2=α^2-(β-x)^2$

$h^2=α^2-β^2+2βx-x^2$

De ces deux relations on obtient l'égalité

$γ^2-x^2=α^2-β^2+2βx-x^2$

$x=\frac(γ^2-α^2+β^2)(2β)$

$h^2=γ^2-(\frac(γ^2-α^2+β^2)(2β))^2$

$h^2=\frac((α^2-(γ-β)^2)((γ+β)^2-α^2))(4β^2)$

$h^2=\frac((α-γ+β)(α+γ-β)(γ+β-α)(γ+β+α))(4β^2)$

Puisque $ρ=\frac(α+β+γ)(2)$, alors $α+β+γ=2ρ$, ce qui signifie

$h^2=\frac(2ρ(2ρ-2γ)(2ρ-2β)(2ρ-2α))(4β^2)$

$h^2=\frac(4ρ(ρ-α)(ρ-β)(ρ-γ))(β^2 )$

$h=\sqrt(\frac(4ρ(ρ-α)(ρ-β)(ρ-γ))(β^2))$

$h=\frac(2)(β)\sqrt(ρ(ρ-α)(ρ-β)(ρ-γ))$

D'après le théorème 1, on obtient

$S=\frac(1)(2) βh=\frac(β)(2)\cdot \frac(2)(β) \sqrt(ρ(ρ-α)(ρ-β)(ρ-γ) )=\sqrt(ρ(ρ-α)(ρ-β)(ρ-γ))$

Parfois, dans la vie, il y a des situations où vous devez fouiller dans votre mémoire à la recherche de connaissances scolaires oubliées depuis longtemps. Par exemple, vous devez déterminer la superficie d'un terrain de forme triangulaire, ou le moment est venu de procéder à une autre rénovation dans un appartement ou une maison privée, et vous devez calculer la quantité de matériau nécessaire pour une surface avec une forme triangulaire. Il fut un temps où vous pouviez résoudre un tel problème en quelques minutes, mais maintenant vous essayez désespérément de vous rappeler comment déterminer l'aire d'un triangle ?

Ne vous inquiétez pas ! Après tout, il est tout à fait normal que le cerveau d’une personne décide de transférer des connaissances longtemps inutilisées quelque part vers un coin éloigné, d’où il n’est parfois pas si facile de les extraire. Pour que vous n'ayez pas à chercher des connaissances scolaires oubliées pour résoudre un tel problème, cet article contient diverses méthodes qui facilitent la recherche de l'aire requise d'un triangle.

Il est bien connu qu’un triangle est un type de polygone limité au nombre minimum de côtés possible. En principe, tout polygone peut être divisé en plusieurs triangles en reliant ses sommets par des segments qui ne coupent pas ses côtés. Par conséquent, connaissant le triangle, vous pouvez calculer l'aire de presque n'importe quelle figure.

Parmi tous les triangles possibles qui apparaissent dans la vie, on peut distinguer les types particuliers suivants : et rectangulaires.

La façon la plus simple de calculer l'aire d'un triangle est lorsqu'un de ses angles est droit, c'est-à-dire dans le cas d'un triangle rectangle. Il est facile de voir qu’il s’agit d’un demi-rectangle. Son aire est donc égale à la moitié du produit des côtés qui forment un angle droit entre eux.

Si l'on connaît la hauteur d'un triangle, abaissé d'un de ses sommets jusqu'au côté opposé, et la longueur de ce côté, qui s'appelle la base, alors l'aire est calculée comme la moitié du produit de la hauteur et de la base. Ceci s'écrit à l'aide de la formule suivante :

S = 1/2*b*h, dans lequel

S est l'aire requise du triangle ;

b, h - respectivement, la hauteur et la base du triangle.

Il est si facile de calculer l'aire d'un triangle isocèle car la hauteur divisera le côté opposé en deux et peut être facilement mesurée. Si la surface est déterminée, il est alors pratique de prendre comme hauteur la longueur de l'un des côtés formant un angle droit.

Tout cela est bien sûr bien, mais comment déterminer si l'un des angles d'un triangle est droit ou non ? Si la taille de notre figure est petite, nous pouvons alors utiliser un angle de construction, un triangle de dessin, une carte postale ou un autre objet de forme rectangulaire.

Mais que se passe-t-il si nous avons un terrain triangulaire ? Dans ce cas, procédez comme suit : comptez à partir du haut de l'angle droit supposé d'un côté une distance multiple de 3 (30 cm, 90 cm, 3 m), et de l'autre côté mesurez une distance multiple de 4 dans le même proportion (40 cm, 160 cm, 4 m). Vous devez maintenant mesurer la distance entre les extrémités de ces deux segments. Si le résultat est un multiple de 5 (50 cm, 250 cm, 5 m), alors on peut dire que l'angle est droit.

Si la longueur de chacun des trois côtés de notre figure est connue, alors l'aire du triangle peut être déterminée à l'aide de la formule de Heron. Pour qu'il ait une forme plus simple, une nouvelle valeur est utilisée, appelée demi-périmètre. C'est la somme de tous les côtés de notre triangle, divisés en deux. Une fois le demi-périmètre calculé, vous pouvez commencer à déterminer la superficie à l'aide de la formule :

S = sqrt(p(p-a)(p-b)(p-c)), où

sqrt - racine carrée ;

p - valeur du demi-périmètre (p = (a+b+c)/2) ;

a, b, c - bords (côtés) du triangle.

Mais que se passe-t-il si le triangle a une forme irrégulière ? Il y a deux manières possibles ici. La première consiste à essayer de diviser une telle figure en deux triangles rectangles, dont la somme des aires est calculée séparément, puis additionnée. Ou, si l'angle entre deux côtés et la taille de ces côtés sont connus, alors appliquez la formule :

S = 0,5 * ab * sinC, où

a,b - côtés du triangle ;

c est la taille de l'angle entre ces côtés.

Ce dernier cas est rare dans la pratique, mais néanmoins, tout est possible dans la vie, la formule ci-dessus ne sera donc pas superflue. Bonne chance avec vos calculs!

Aire d'un triangle. Dans de nombreux problèmes de géométrie impliquant le calcul d'aires, des formules pour l'aire d'un triangle sont utilisées. Il en existe plusieurs, nous allons ici examiner les principaux.Énumérer ces formules serait trop simple et inutile. Nous analyserons l'origine des formules de base, celles qui sont les plus souvent utilisées.

Avant de lire la dérivation des formules, assurez-vous de consulter l'article sur.Après avoir étudié le matériel, vous pouvez facilement restaurer les formules dans votre mémoire (si elles « s'envolent » soudainement au moment où vous en avez besoin).

Première formule

La diagonale d'un parallélogramme le divise en deux triangles d'égale aire :

Par conséquent, l'aire du triangle sera égale à la moitié de l'aire du parallélogramme :

Aire de formule du triangle

*C'est-à-dire que si nous connaissons n'importe quel côté du triangle et la hauteur abaissée de ce côté, alors nous pouvons toujours calculer l'aire de ce triangle.

Formule deux

Comme déjà indiqué dans l'article sur l'aire d'un parallélogramme, la formule ressemble à :

L'aire d'un triangle est égale à la moitié de son aire, ce qui signifie :

*C'est-à-dire que si deux côtés d'un triangle et l'angle qui les sépare sont connus, nous pouvons toujours calculer l'aire d'un tel triangle.

Formule du héron (troisième)

Cette formule est difficile à dériver et elle ne vous est d’aucune utilité. Regardez comme elle est belle, vous pouvez dire qu'elle est elle-même mémorable.

*Si trois côtés d'un triangle sont donnés, alors en utilisant cette formule, nous pouvons toujours calculer son aire.

Formule quatre

Où r– rayon du cercle inscrit

*Si les trois côtés d'un triangle et le rayon du cercle qui y est inscrit sont connus, alors on peut toujours trouver l'aire de ce triangle.

Formule cinq

Où R.– rayon du cercle circonscrit.

*Si les trois côtés d'un triangle et le rayon du cercle qui l'entoure sont connus, alors on peut toujours trouver l'aire d'un tel triangle.

La question se pose : si trois côtés d’un triangle sont connus, alors n’est-il pas plus facile de trouver son aire à l’aide de la formule de Héron !

Oui, cela peut être plus facile, mais pas toujours, parfois la complexité surgit. Cela implique d’extraire la racine. De plus, ces formules sont très pratiques à utiliser dans des problèmes où l'aire d'un triangle et ses côtés sont donnés et où vous devez trouver le rayon du cercle inscrit ou circonscrit. De telles tâches sont disponibles dans le cadre de l'examen d'État unifié.

Examinons la formule séparément :

C'est un cas particulier de la formule de l'aire d'un polygone dans lequel est inscrit un cercle :

Considérons cela en utilisant l'exemple d'un pentagone :

Relions le centre du cercle aux sommets de ce pentagone et aux perpendiculaires inférieures du centre à ses côtés. Nous obtenons cinq triangles, les perpendiculaires tombées étant les rayons du cercle inscrit :

L'aire du pentagone est :

Or il est clair que si nous parlons d'un triangle, alors cette formule prend la forme :

Formule six